How Do You Know if a Graph Has a Vertical Asymptote

Evidence Mobile Notice Show All NotesHide All Notes

Mobile Find

You appear to be on a device with a "narrow" screen width (i.due east. you lot are probably on a mobile phone). Due to the nature of the mathematics on this site it is best views in landscape mode. If your device is not in mural mode many of the equations will run off the side of your device (should exist able to scroll to see them) and some of the card items will exist cut off due to the narrow screen width.

Section 4-viii : Rational Functions

In this concluding section nosotros need to discuss graphing rational functions. Information technology'south is probably best to showtime off with a fairly uncomplicated one that we tin can practice without all that much knowledge on how these piece of work.

Let's sketch the graph of \(f\left( ten \right) = \frac{i}{x}\). First, since this is a rational function we are going to take to be careful with sectionalization past zero issues. So, we tin come across from this equation that nosotros'll have to avoid \(10 = 0\) since that will give division by zero.

Now, permit's just plug in some values of \(x\) and run into what nosotros become.

\(x\)	\(f(ten)\)
-4	-0.25
-two	-0.5
-1	-i
-0.1	-10
-0.01	-100
0.01	100
0.ane	ten
1	1
2	0.five
4	0.25

So, equally \(10\) become large (positively and negatively) the office keeps the sign of \(x\) and gets smaller and smaller. Likewise, equally nosotros approach \(ten = 0\) the function once again keeps the same sign as \(x\) simply starts getting quite large. Here is a sketch of this graph.

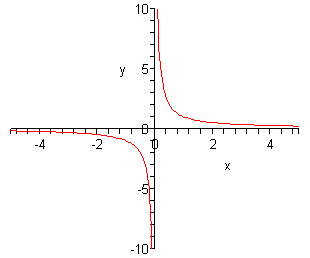
First, notice that the graph is in 2 pieces. Almost all rational functions will have graphs in multiple pieces like this.

Side by side, notice that this graph does not have any intercepts of whatsoever kind. That's easy plenty to check for ourselves.

Think that a graph volition take a \(y\)-intercept at the point \(\left( {0,f\left( 0 \correct)} \right)\). However, in this case nosotros accept to avoid \(10 = 0\) and and then this graph will never cross the \(y\)-axis. It does get very close to the \(y\)-axis, but it will never cantankerous or touch it and and so no \(y\)-intercept.

Side by side, recollect that nosotros tin can determine where a graph volition have \(x\)-intercepts past solving \(f\left( ten \right) = 0\). For rational functions this may seem like a mess to bargain with. However, there is a nice fact well-nigh rational functions that we can use here. A rational office will be zilch at a particular value of \(x\) but if the numerator is zero at that \(ten\) and the denominator isn't zip at that \(x\). In other words, to make up one's mind if a rational function is ever aught all that nosotros demand to do is set the numerator equal to cypher and solve. Once we have these solutions nosotros simply demand to bank check that none of them make the denominator zippo likewise.

In our case the numerator is one and will never exist zero and and so this role will accept no \(ten\)-intercepts. Again, the graph will get very close to the \(ten\)-axis but it will never touch or cross it.

Finally, we need to address the fact that graph gets very close to the \(10\) and \(y\)-axis merely never crosses. Since there isn't anything special about the axis themselves we'll employ the fact that the \(10\)-centrality is really the line given by \(y = 0\) and the \(y\)-axis is really the line given past \(x = 0\).

In our graph as the value of \(ten\) approaches \(x = 0\) the graph starts gets very large on both sides of the line given by \(ten = 0\). This line is called a vertical asymptote.

Also, every bit \(x\) become very big, both positive and negative, the graph approaches the line given by \(y = 0\). This line is called a horizontal asymptote.

Here are the general definitions of the two asymptotes.

1. The line \(x = a\) is a vertical asymptote if the graph increases or decreases without spring on i or both sides of the line as \(x\) moves in closer and closer to \(x = a\).
2. The line \(y = b\) is a horizontal asymptote if the graph approaches \(y = b\) as \(x\) increases or decreases without jump. Note that it doesn't take to approach \(y = b\) as \(x\) BOTH increases and decreases. It just needs to approach it on one side in order for information technology to exist a horizontal asymptote.

Determining asymptotes is actually a fairly simple process. First, let's commencement with the rational office,

\[f\left( x \right) = \frac{{a{10^northward} + \cdots }}{{b{x^k} + \cdots }}\]

where \(north\) is the largest exponent in the numerator and \(m\) is the largest exponent in the denominator.

Nosotros then have the following facts most asymptotes.

1. The graph volition have a vertical asymptote at \(10 = a\) if the denominator is naught at \(x = a\) and the numerator isn't cypher at \(ten = a\).
2. If \(n < m\) then the \(x\)-axis is the horizontal asymptote.
3. If\(northward = m\) and so the line \(\displaystyle y = \frac{a}{b}\) is the horizontal asymptote.
4. If \(due north > m\) in that location will be no horizontal asymptotes.

The procedure for graphing a rational part is fairly simple. Here it is.

Procedure for Graphing a Rational Role

1. Find the intercepts, if there are any. Call up that the \(y\)-intercept is given by \(\left( {0,f\left( 0 \right)} \right)\) and we find the \(ten\)-intercepts past setting the numerator equal to goose egg and solving.
2. Notice the vertical asymptotes past setting the denominator equal to zero and solving.
3. Find the horizontal asymptote, if it exists, using the fact above.
4. The vertical asymptotes will split up the number line into regions. In each region graph at least one point in each region. This point will tell the states whether the graph volition be above or below the horizontal asymptote and if we need to nosotros should go several points to determine the general shape of the graph.
5. Sketch the graph.

Note that the sketch that we'll get from the process is going to be a adequately rough sketch just that is okay. That's all that nosotros're really after is a bones idea of what the graph will expect at.

Permit'due south take a look at a couple of examples.

Example 1 Sketch the graph of the following office. \[f\left( x \right) = \frac{{3x + 6}}{{x - 1}}\]

Prove Solution

So, we'll first off with the intercepts. The \(y\)-intercept is,

\[f\left( 0 \right) = \frac{6}{{ - 1}} = - vi\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( {0, - 6} \right)\]

The \(10\)-intercepts will be,

\[\begin{align*}3x + 6 & = 0\\ x & = - ii\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( { - 2,0} \right)\terminate{marshal*}\]

Now, we demand to determine the asymptotes. Let'south start find the vertical asymptotes.

\[ten - 1 = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}ten = i\]

And then, we've got i vertical asymptote. This means that in that location are now ii regions of \(x\)'s. They are \(10 < 1\) and \(10 > one\).

Now, the largest exponent in the numerator and denominator is 1 then by the fact there will be a horizontal asymptote at the line.

\[y = \frac{iii}{1} = 3\]

Now, we only need points in each region of \(ten\)'due south. Since the \(y\)-intercept and \(ten\)-intercept are already in the left region nosotros won't need to get any points at that place. That means that we'll just need to go a point in the right region. It doesn't actually matter what value of \(x\) we option here nosotros simply need to keep it fairly small so it will fit onto our graph.

\[f\left( 2 \right) = \frac{{3\left( ii \correct) + 6}}{{2 - 1}} = \frac{{12}}{1} = 12\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( {2,12} \right)\]

Okay, putting all this together gives the following graph.

Note that the asymptotes are shown every bit dotted lines.

Instance ii Sketch the graph of the following function. \[f\left( x \right) = \frac{nine}{{{ten^two} - ix}}\]

Show Solution

Okay, nosotros'll outset with the intercepts. The \(y\)-intercept is,

\[f\left( 0 \right) = \frac{9}{{ - nine}} = - 1\hspace{0.25in} \Rightarrow \hspace{0.25in}\left( {0, - 1} \correct)\]

The numerator is a abiding and so there won't be any \(x\)-intercepts since the role can never exist zero.

Next, we'll have vertical asymptotes at,

\[{x^ii} - 9 = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}10 = \pm 3\]

So, in this case we'll have three regions to our graph : \(x < - three\), \( - 3 < x < 3\), \(x > iii\).

Also, the largest exponent in the denominator is 2 and since in that location are no \(ten\)'south in the numerator the largest exponent is 0, and then by the fact the \(x\)-centrality will be the horizontal asymptote.

Finally, we need some points. We'll utilise the post-obit points here.

\[\begin{align*}f\left( { - 4} \right) & = \frac{9}{7} & \hspace{0.25in} & \left( { - 4,\frac{9}{7}} \right)\\ f\left( { - two} \right) & = - \frac{9}{five} & \hspace{0.25in} & \left( { - 2, - \frac{9}{5}} \correct)\\ f\left( 2 \right) & = - \frac{9}{5} & \hspace{0.25in} & \left( {2, - \frac{9}{5}} \right)\\ f\left( 4 \correct) & = \frac{9}{vii} & \hspace{0.25in} & \left( {4,\frac{9}{7}} \right)\end{align*}\]

Notice that along with the ­\(y\)-intercept nosotros actually have iii points in the middle region. This is because at that place are a couple of possible behaviors in this region and we'll need to decide the actual beliefs. We'll see the other main behaviors in the next examples and then this will make more sense at that point.

Here is the sketch of the graph.

Example iii Sketch the graph of the following role. \[f\left( x \right) = \frac{{{ten^2} - 4}}{{{x^2} - 4x}}\]

Evidence Solution

This fourth dimension find that if nosotros were to plug in \(10 = 0\) into the denominator nosotros would get partitioning by zero. This means there will not be a \(y\)-intercept for this graph. We have however, managed to find a vertical asymptote already.

Now, allow's run into if we've got \(ten\)-intercepts.

\[{x^2} - 4 = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}ten = \pm 2\]

And then, we've got 2 of them.

We've got one vertical asymptote, but there may be more than so permit'southward go through the process and run across.

\[{10^2} - 4x = x\left( {x - 4} \right) = 0\hspace{0.25in} \Rightarrow \hspace{0.25in}10 = 0,\,\,x = 4\]

And so, we've got two again and the three regions that nosotros've got are \(x < 0\), \(0 < x < 4\) and \(x > 4\).

Side by side, the largest exponent in both the numerator and denominator is ii so by the fact there volition exist a horizontal asymptote at the line,

\[y = \frac{ane}{i} = 1\]

Now, i of the \(x\)-intercepts is in the far left region so we don't need any points in that location. The other \(x\)-intercept is in the middle region. So, we'll need a point in the far right region and every bit noted in the previous example nosotros will want to get a couple more points in the center region to completely decide its behavior.

\[\begin{marshal*}f\left( 1 \right) & = 1 & \hspace{0.25in} & \left( {ane,1} \right)\\ f\left( 3 \right) & = - \frac{5}{3} & \hspace{0.25in} & \left( {3, - \frac{5}{iii}} \right)\\ f\left( 5 \right) & = \frac{{21}}{five} & \hspace{0.25in} & \left( {v,\frac{{21}}{five}} \right)\end{align*}\]

Here is the sketch for this office.

Notice that this time the middle region doesn't have the aforementioned behavior at the asymptotes equally nosotros saw in the previous case. This tin can and will happen fairly oftentimes. Sometimes the behavior at the two asymptotes will be the same as in the previous example and sometimes it will accept the reverse behavior at each asymptote as we see in this example. Considering of this we will always need to get a couple of points in these types of regions to determine just what the behavior will exist.

terryolower.blogspot.com

Source: https://tutorial.math.lamar.edu/classes/alg/graphrationalfcns.aspx

Share this post